In today’s data-driven world, logistic regression is a key tool for predictive modeling. It’s used for tasks where the outcome is either yes or no. Unlike linear regression, which predicts continuous values, logistic regression uses a special function to guess the chance of a yes or no answer.
Logistic regression is all about probability. It tries to figure out the chance that something will happen. This method uses a special way to find these probabilities, making it great for real-world problems.
The logistic function is special because it turns numbers into chances between 0 and 1. This is different from linear regression, which predicts numbers and uses a simple line to fit the data.
Logistic regression is very useful and can be used in many ways. It’s used in health, finance, and more. It helps make clear decisions by turning complex data into simple yes or no answers.
Key Takeaways:
- Logistic regression is a statistical model tailored for binary classification problems, unlike linear regression that targets continuous ooutcomes.
- Through the use of a logistic function, it converts logistic odds into probabilities between 0 and 1, making it ideal for probability modeling.
- The model relies on maximum likelihood estimation, which provides a robust framework for parameter estimation.
- Logistic regression is highly versatile and can be adapted for multinomial and ordinal dependent variables.
- The technique is entrenched in the concept of maximum entropy, striving to infer as much as possible with the least unwarranted assumptions.
- Its real-world applications span from making diagnostic predictions in healthcare to forecasting financial risks and consumer behavior.
Understanding the Fundamentals of Logistic Regression:
Logistic regression is a key method in predictive analytics and machine learning. It’s great for tasks where you have two outcomes. It uses the logistic function to guess the chance of something happening.
What is a Logistic Function?:
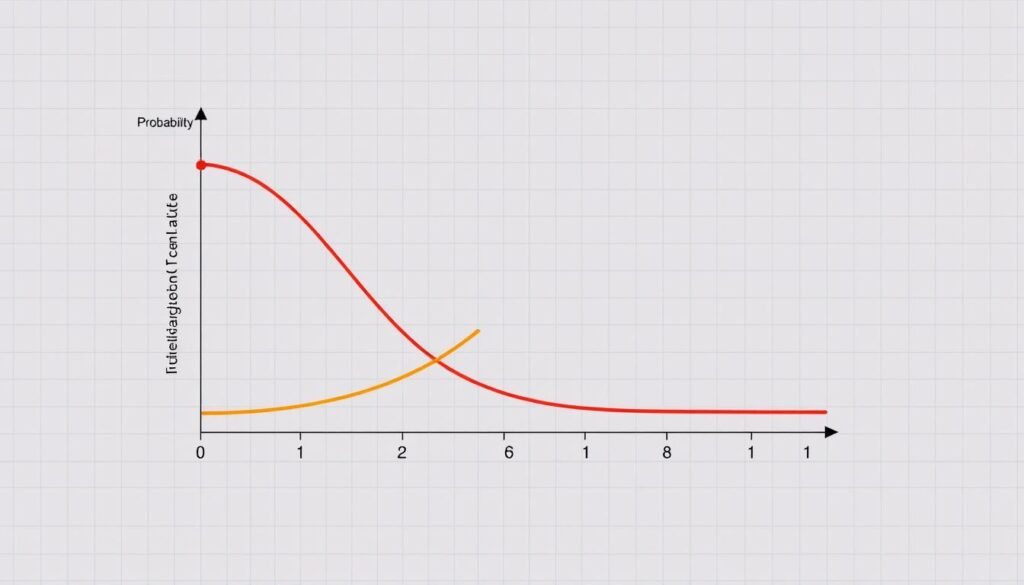
The logistic function is at the heart of logistic regression. It creates an S-shaped curve, also known as the sigmoid function. This curve turns any number into a value between 0 and 1. It’s perfect for tasks where you have only two choices, like “yes” or “no”. The function makes sure the output is always between 0 and 1. This fits well with binary choices.
Key Components of Logistic Regression:
Logistic regression has several important parts. These include independent variables, the logistic function, odds and log-odds, coefficients, and maximum likelihood estimation. Together, they help the model make predictions and classify data into two groups.
Basic Mathematical Concepts:
The math behind logistic regression is based on the logit transformation. The logit is the natural logarithm of the odds ratio. It connects the probability of an event to its predictors.
Logistic regression is often used in supervised learning for binary data. The process starts with preparing the data. Then, the model is trained to find the best parameters using maximum likelihood. Lastly, the model is tested.
Logistic regression is strong for modeling binary outcomes. It’s used for predicting customer churn or medical diagnoses. It provides a solid way to make predictions based on probabilities.
Linear Regression vs. Logistic Regression: Key Differences:
In the world of supervised machine learning, it’s important to know the difference between linear and logistic regression. Both are used for predictive modeling, but they work with different types of data. This leads to different results, depending on the nature of the outcome variable.
Continuous vs. Categorical Outcomes:
Linear regression is for continuous data. It predicts a continuous outcome from input variables. For example, it can forecast the temperature based on past weather data.
On the other hand, logistic regression is for categorical outcomes, like binary ones. It predicts if an email is spam or not. The output is a probability between 0 and 1, thanks to the logistic function.
Line of Best Fit vs. S-Curve:
Linear regression finds a straight line that best fits the data. It uses the least square error method. In contrast, logistic regression uses an S-curve to represent the probability of a binary outcome.
This S-curve is key in setting a decision boundary in classification algorithms.
Interpretation of Results:
Interpreting the results of these regressions is different. Linear regression directly predicts values, like house prices based on size and location. Logistic regression, on the other hand, gives a probability of an event happening, like tumor malignancy based on medical inputs. Choosing between linear and logistic regression depends on understanding these differences. For a deeper look, check out this detailed comparison between linear and logistic regression.
The Mathematics Behind the Logit Model:
The core of logistic regression is the logit transformation. It changes log odds into probabilities. This is key for understanding how the model works, important in fields like medicine and marketing.
The sigmoid function is at the heart of this. It takes input values and turns them into outputs between 0 and 1. This is essential for predicting probabilities, like yes/no answers, in probability modeling.
Maximum likelihood estimation (MLE) is vital in the logit model. It finds the best fit for the data by maximizing the likelihood of observing it. This method is great for models without a simple solution.
MLE is a big help in logistic regression. It adjusts parameters to find the most likely outcomes. This makes it a strong tool for probability modeling.
Grasping the math behind logistic regression improves data analysis. It also makes predictions more accurate in many fields.
Types of Logistic Regression Models:
In supervised learning, logistic regression is a key tool for classification. It’s great for binary classification, multinomial classification, and predicting ordered outcomes. Let’s look at the different types of logistic regression models. They’re designed to handle different types of categorical responses well.
Binary Logistic Regression:
Binary logistic regression is the simplest type. It’s perfect for tasks with only two outcomes. This includes email spam detection and medical diagnosis, where the answer is yes or no, or true or false. The model finds the probability of each outcome and turns it into a binary result.
Multinomial Logistic Regression:
Multinomial logistic regression is for more than two classes without any order. It’s great for tasks like predicting crop diseases or classifying documents. This model uses the log odds of each class to make predictions.
Ordinal Logistic Regression:
Ordinal logistic regression is for when the categories have a natural order but the gaps between them are not the same. It’s used in educational grading, service satisfaction, or disease stages. This model sees the ordered levels as having a logical sequence, which affects the predictions.
| Type of Model | Predictive Outcome | Common Use-case |
|---|---|---|
| Binary Logistic Regression | Binary (0 or 1) | Fraud detection |
| Multinomial Logistic Regression | Multiple classes (unordered) | Document categorization |
| Ordinal Logistic Regression | Ordered classes | Rating customer satisfaction |
Logistic regression models are key in supervised learning. They’re tailored for specific types of categorical data and needs. This shows their importance in various fields.
Understanding Probability and Odds Ratios:
Logistic analysis relies on probability modeling and odds ratios. These are key for precise logistic regression. They help us understand data, focusing on event outcomes.
Converting Probabilities to Odds:
It’s important to know how to switch from probabilities to odds. Probabilities range from 0 to 1, showing how likely something is to happen. Odds, on the other hand, compare the chance of an event happening to it not happening.
For example, a 0.75 probability means the odds are 3:1. This shows the event is three times more likely to happen than not.
Interpreting Odds Ratios:
Odds ratios are a big deal in logistic analysis. They compare the odds of an event happening under different conditions. This is really useful for binary outcomes in logistic regression.
An odds ratio of 3.71 in medical treatment means something. It shows the odds of a bad outcome with standard treatment are 3.71 times higher than with a new treatment. This gives a clear measure of how treatments compare.
Maximum Likelihood Estimation
Maximum likelihood estimation (MLE) is essential for fitting logistic regression models. It picks the best parameter values (coefficients) for the model. This makes sure the model fits the data well.
Logistic regression is great for complex data with categorical outcomes. It uses MLE and odds ratios for better insights and predictions. This makes it a powerful tool for researchers and statisticians.
Model Evaluation and Goodness of Fit:
In logistic regression, a strong goodness of fit is key for reliable models. A good fit means the model accurately predicts outcomes. The Hosmer-Lemeshow test is a common way to check this, but it can be tricky with big samples.
There’s a better way to use the Hosmer-Lemeshow test, making it work for all sample sizes. This method adds a special parameter to check fit, not just size. Also, using graphs and subsampling is smart for big data, as they show how well the model fits.
Logistic regression is used in many areas, like predicting cataract risk or checking mortality in critical care. These uses make sure models are not just numbers but also useful in real life. For more on this, check out Linear Regression Analysis.
Today, experts suggest mixing the modified Hosmer-Lemeshow test with graphs. This mix helps deal with big data and shows how well the model works in real life.
| Method | Goodness of Fit Evaluation | Applicability in Sample Size |
|---|---|---|
| Traditional Hosmer-Lemeshow Test | May mislead in large samples | Less effective as sample size increases |
| Modified Hosmer-Lemeshow | Standardizes power, reducing false positives | Effective across varying sample sizes |
| Graphical Methods & Subsampling | Provides visual and statistical calibration | Highly effective in large datasets |
Using these advanced model evaluation methods can greatly improve logistic regression models. This makes predictions more accurate and reliable, boosting the model’s overall performance.
Real-World Applications and Use Cases:
Logistic regression is very useful in many areas. It helps make predictions for binary classification. This is important for making decisions in different fields. Here are some examples:
Medical Diagnosis:
In medicine, logistic regression is key for predicting diseases. It looks at patient data to guess if someone might have a disease. This helps doctors plan early treatments.
Financial Risk Assessment:
Logistic regression helps banks predict if someone will pay back a loan. This makes lending safer and more informed. It’s all about managing financial risks.
Marketing and Customer Behavior:
Marketers use logistic regression to guess what customers will do. This helps them make better ads and products. It’s all about understanding what people want to buy.
Social Sciences Research:
In social sciences, logistic regression is used to study things like voting and policy acceptance. It helps researchers understand big trends. This gives us insights into how people behave together.
Here’s a table showing how logistic regression is used in medicine and finance:
| Field | Use Case | Example |
|---|---|---|
| Medical | Disease Prediction | Predicting heart disease occurrence from patient biometrics. |
| Finance | Credit Scoring | Assessing creditworthiness to make loan approval decisions. |
| Marketing | Customer Segmentation | Predicting which users are likely to purchase a new product. |
| Social Science | Policy Analysis | Evaluating the acceptance rate of new government policies. |
Logistic regression is very important. It helps us make better decisions by using data. This makes things more efficient and effective in many areas.
Common Challenges and Limitations:
Logistic regression is widely used but faces several challenges. These include overfitting, sample size, and multicollinearity. Knowing these issues helps in using logistic regression more effectively.
Overfitting Issues:
Overfitting happens when a model fits the training data too well but fails with new data. This often occurs with complex models and small datasets. To fix this, regularization like Lasso (L1) and Ridge (L2) is used. These methods reduce large coefficients in the model.
Sample Size Requirements:
The size of the sample is key for logistic regression to work well. A small sample can lead to bad estimates and predictions. Luckily, logistic regression can work with a small sample size, making it useful for many fields. But, having enough data is essential for reliable predictions.
Multicollinearity:
Multicollinearity is when variables are too closely related. This makes the model’s estimates less accurate. To spot this, variance inflation factors (VIF) are used. It can be fixed by removing variables or using regularization.
Here’s a table showing the challenges and how to solve them:
| Challenge | Impact | Mitigation Strategy |
|---|---|---|
| Overfitting | Model fails to generalize | Implement regularization (L1, L2) |
| Sample Size | Inaccurate estimates | Increase sample size, use robust techniques |
| Multicollinearity | Distorted estimates | Variable removal, regularization |
Implementing Logistic Regression in Machine Learning:
In supervised machine learning, logistic regression is key for solving binary problems. We’ll explore how to train the model, pick the right features, and use regularization techniques. These steps improve the logistic regression implementation.
Model Training Process:
The training process starts with splitting data into training and test sets. It’s important to handle both numbers and categories well. Then, gradient descent comes into play. It tweaks the model’s parameters to get closer to the real results, making the model better and faster.
Feature Selection:
Picking the right features is critical for logistic regression. It’s about choosing the most important variables that affect the outcome. This makes the model simpler, faster, and more reliable, avoiding overfitting problems.
Regularization Techniques:
To fight overfitting, regularization techniques like L1 and L2 are used. They adjust the model’s coefficients, adding a penalty for complexity. This not only simplifies the model but also boosts its accuracy on new data.
By following these steps, from gradient descent to feature selection and regularization techniques, we create a strong logistic regression implementation. It’s designed to predict outcomes with great accuracy.
Conclusion:
In the world of supervised learning, logistic regression is a key classification algorithm. It’s known for its important role in predictive modeling. It’s used for both binary and multinomial classification tasks.
Logistic regression uses a special function to model probabilities. This ensures the outputs are always between 0 and 1. We’ve seen how it differs from linear regression, focusing on categorical outcomes and having a unique S-curve.
Logistic regression is valued for its simplicity and wide use in fields like healthcare and finance. It’s great for binary classification. It can turn probabilities into odds ratios, making results easier to understand.
But, it relies on certain assumptions and needs good data preparation. It’s also important to use the right metrics to check how well the model works. This includes the confusion matrix, ROC-AUC curve, and F1-score.
Using logistic regression involves careful steps. You need to check its assumptions, prepare your data well, and evaluate its performance. When done right, it’s a powerful tool for making smart decisions.
Even with its limitations, logistic regression is useful. It can handle both continuous and categorical inputs. It also gives clear probabilities as outputs. This makes it a reliable choice in data analysis.
